ゴーリストのチナパです!この度は技術的な記事ではなく、「AIに任せましょう」などを聞くときに、実際に何が起きているのかの直感を作るための記事です。(プログラミングなしです)
データでモデルを学習しそして分類の判断を行う時に、何かの規則を作ってから判断しているのが事実です。複雑な問題であるほど人間の頭で想像しにくくなるかも知れませんが、直感を作ることはできます。

Public Domain Pictures · Photography
簡単な問題でやってみよう
この度はhttps://playground.tensorflow.org, という実験できる場所から始めましょう。ここでは、ノープログラミングでニューラルネットと遊べます。

初めての方だと、色々がありすぎてびっくりするかも知れませんが、一歩ずつ進めて行きます!
スタート地点はこちらです。左側の「Data」のところで、写真の通り、一番簡単なデータを選びましょう。すると、右側の「Output」にそれが反映されます。(一旦、左のメニューにNoiseも0%だと確認しましょう)。

これは二次元のグラフですのでちゃんと二つの軸があります、x軸とy軸と言われてる時もありますが、こちらで横軸がX1と縦軸がX2です。この二つを私たちが測ってます(この場合はランダムで作られてるけど、現実の状況であれば測っていたりしている)。点の種類は二つあります、オレンジと青、そしてこの例ではご覧の通り綺麗な二つの固まりになってます。
計算機を使うまでもなく、オレンジの点がX1=-2, X2=-2あたりが平均みたいだし、青の点がX1=2, X2=2の周りに集中されてます。 さて、こんな簡単の問題には機械学習がどう解決するのかも見てみましょう。上のあたりのPlayボタンを押してみてください。
押してから、すぐグラフが綺麗なオレンジと青に分けれれていきます。一瞬にでもこのパターンが見抜かれてます。ま、簡単だしな。

グラフに左がわがオレンジになり、右側が青になりました。そして、斜め白い線がオレンジ組と青くみの間を通ってます。
「この二つの組みを分けてください」と子供に聞いたら、似たような線も書いたかも知れません。この場合、この白い一直線が「決定境界」と言います。 白い線の左はオレンジ、右が青。つまり、この線によって判断されてます。
ちょっとずるいことをしてみましょう。
こんな簡単な問題にも、情報が足りなかったら、良い判断が一気にとりにくくなります。

「Features」の下にあるX1の変数あたりをクリックしたら、色が薄めます。これで、今回はX1の情報は機械学習のモデルに渡さないことになってます。つまり、縦軸であるX2の情報だけで、点がオレンジなのか、青なのかを判断しないといけない状況です。またPlayをおし、結果をみましょう。

今度はグラフが横に分けられてます。過ちもあるかも知れません(私の場合、一つの青点がオレンジ背景の部分にあります。なぜなら、縦軸のX2の情報しか得てないため、その情報だけで判断されてるからです。だら、横線になってます。
つまり、決定境界が使ってる変数(Feature、情報)にとても影響されます。
ま、今のところはわかりやすい、ほとんど一直線の例しかみてないので、ハードルを高くしましょう。
渦巻(ナルト?)の出番
X1をもう一回クリックし、モデルにこの情報を与えましょう。ただし、Dataの部分で右下にある渦巻みたいな物を選びましょう。そして、Noiseも入れましょう(私は30%にしましたが、お好きに選んでください)。

Playを押したら….

全然分からない、と言わんばかりのうすい背景と白い横線の決定境界… このうすい色は「自信度が低い」という意味です。学生に聞いて 「なんか…上の辺にオレンジがもう少しあるから…こっちがオレンジになるかな…?」みたいな答えです。
ま…一直線を書いてこのデータを分類するのが不可能だからです。渦巻だから。 では、どうしたら一直線ではない決定境界を作ることができます?
方法があります。 「Feature」の項目で一直線ではないデータで一直線的ではないデータを含めること。
Featureの項目で一番したにあるsin(X1)とsin(X2)も選択して、同じネットワークをplayしましょう。

一気に、決定境界がとんでもないことになってます。

しかも、割とあってるし。一体どうやってここまで分かったでしょう?「渦巻」と分かったのか?
ニューラルネットの中身の分析
ここで、真ん中にある「hidden layer」の部分を見てみましょう。

このネットワークには2つにhidden layerがあります。一つ目には4つの「ニューロン」(神経)があって、2つめは2つの「ニューロン」があります。それぞれのものが何を「気づいている」 のかを見るために、マウスを上にホバーしましたら、右のグラフでそのニューロンのアウトプットが観れます。
みなさんとは少し違うかも知れませんが、私の場合最初のhidden layerでは、四つの「気づき」があるみたいです。

1番と2番がとても似ています。これは、sinグラフみたいな波があるようです。この上にはオレンジ、下には青。ですが、これだけでは渦巻にはなりません。
3番目の「気づき」は上から下の階層一番上にはオレンジ、次は青、次はオレンジ、一番したは青。この中には、青が左肩よりだとオレンジは右肩よりだとも気づいているみたです、面白い。 どうやってこれができたのかが気になりましたら、このニューロンに入っていく線をホバーしてみると”weight is 〇〇”みたいのものがあります。
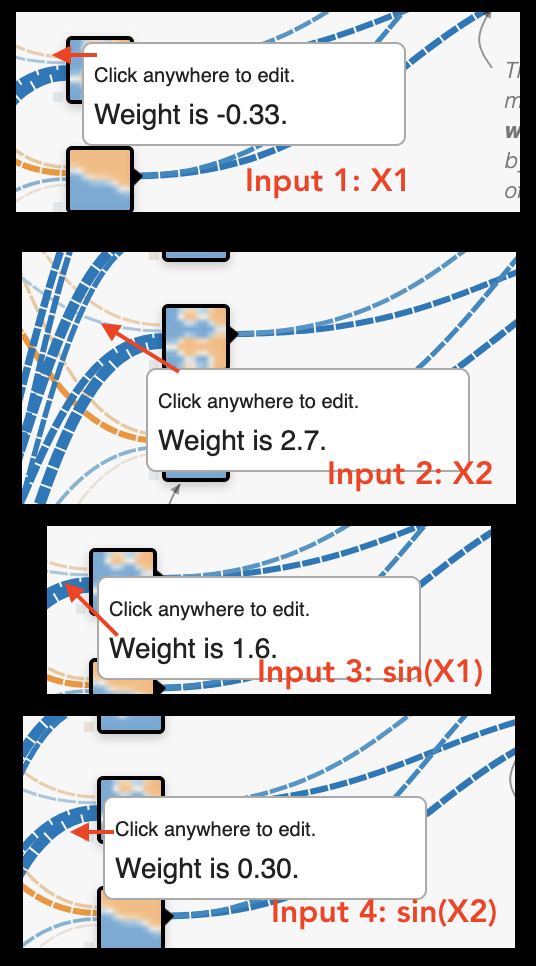
ここでは、(-0.33 x X1) + (0.3 x X2) + (sin(X1) x 1.6) + (sin(X2) x 2.7)のようにこのグラフが作られてますが、数学はそこまでとしましょう。
4番目もX2の逆に似ていて、とりあえず上がオレンジ、下が青と気づいています。
この4つの気づいきを更に組み合わせて、2番のhidden layer にアウトプットを得て、またそのアウトプットを組み合わせて、結果の「渦巻」のようなデータを割と精度高く分類することができる決定境界を描くことができました。
まとめ
ここでX1とX2しか使わなかったため、綺麗な二次元グラフで写すこともできましたが、ディープラーニングのより複雑な分類問題も、結果的に似ているようなことをやっています。フィーチャ数が大きければ大きいほど描きにくい決定境界になりますし、それでこそ便利な道具になっていくこともあります。
例えば...
では、他の種類のデータも、遊んで観てください!hidden layer数を増やして、減らして影響を見ることもできますので、分類で使うdeep learningがどのような決定境界を作ることができるのかの直感がこれでできましたら幸いです。